BCS1130-7&8 Relations (1 & 2)

Lecture notes

• Relation definition
• Relation diagrams
• Reflective relations
• Symmetric relations
• Transitive relations
• Equivalence relations
  • Example
• Anti-symmetry
  • Examples
  • Symmetry vs. Anti-symmetry
• Partial order
  • Examples
• Total order

---

Relation definition

Definition

A relation R describes the relationship between different elements of a given set A: Formal: A relation R on a set A is a subset of the product set $A\times A$

$xRy$

Example: $A=\{1,2,3\}$ → $xRy$ if $x\le y$

Relation diagrams

---

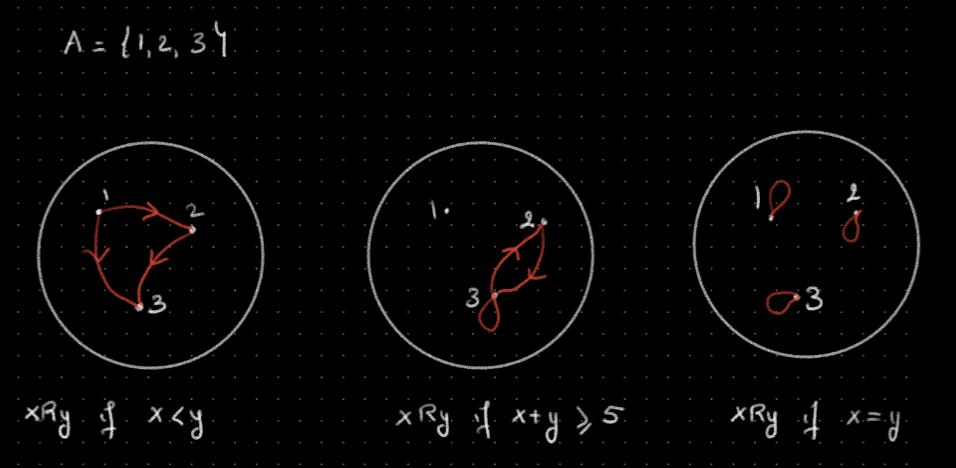
Reflective relations

Definition

A relation R on a set A is reflexive if every element of A is related to itself: $\forall x\in A:xRx$

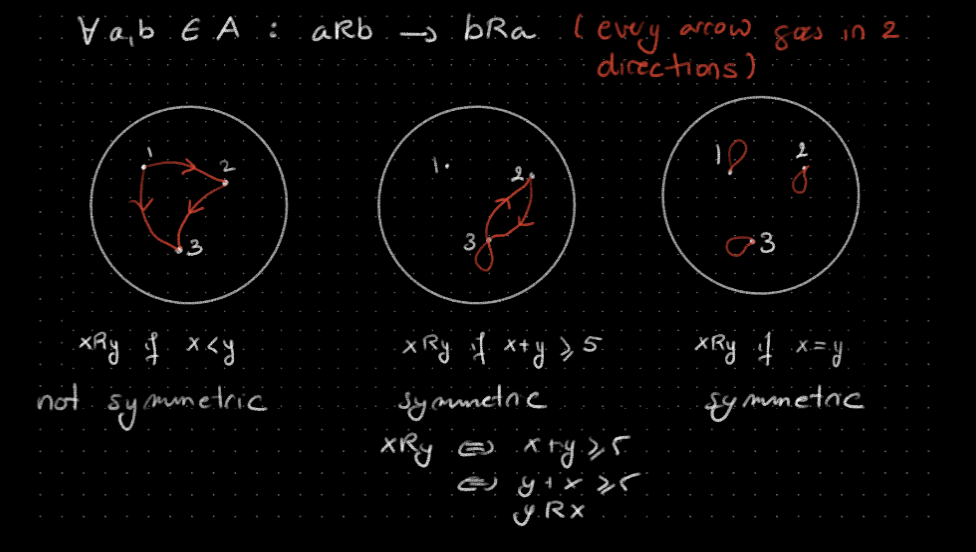
Symmetric relations

Definition

A relation R on a set A is symmetric if for all elements a,b in A: $aRb\to bRa$ $\forall a,b\in A:aRb\to bRa$

Transitive relations

Definition

A relation R on a set A is transitive if for all elements a,b,b in A: $(aRb\wedge bRc)\to aRc$

---

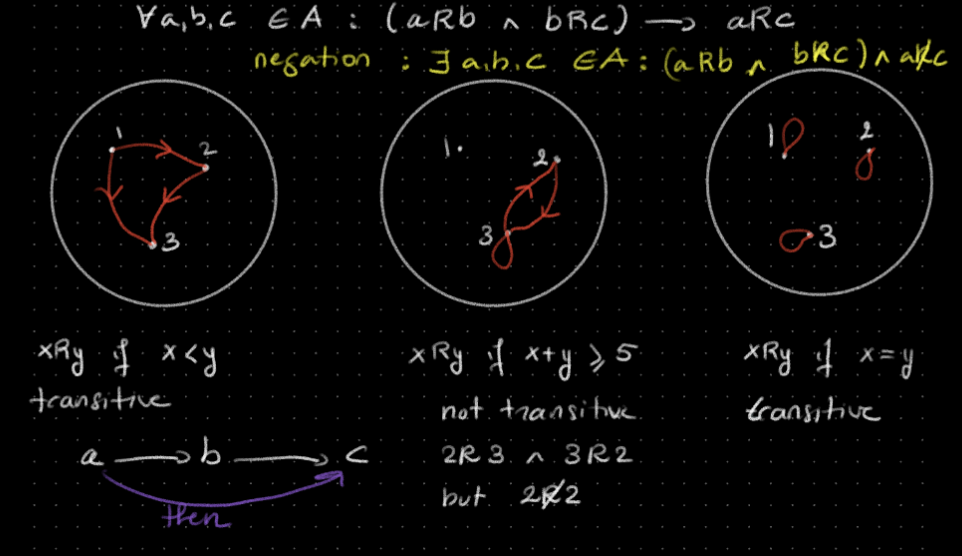
Equivalence relations

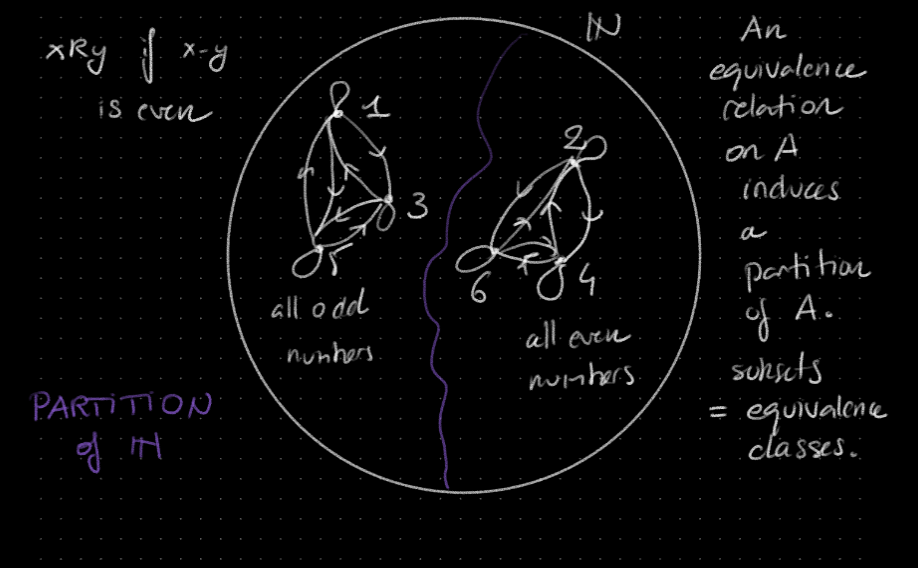
Definition

A relation R is called an equivalence relation if it is reflexive, symmetric and transitive

• An equivalence relation corresponds to a ==partition== of the set
• If you have a partition of a set, you get an equivalence relation

Example Let $A=\mathbb{N}$

• $xRy$ if $x-y$ is even
• Reflexive: $\forall x\in A:xRx$
  • Let $x\in N.x-x=0$ is even → $xRx$ is verified ✅
• Symmetric: $\forall x,y\in A:xRy\to yRx$
  • Assume $x,y\in N,xRy$ then $x-y$ is even
  • then $y-x$ is even (opposite of an even number is also even)
  • so $yRx$ and the relation is symmetric ✅
• Transitive: $\forall x,y,z\in A:(xRy\wedge yRz)\to xRz$
  • Assume $x,y,z\in N,xRy\wedge yRz$
  • then $x-y$ is even and $y-z$ is even
  • then $(x-y)+(y-z)$ is even (sum of even numbers is even)
  • $(x-y)+(y-z)=x-z$ then $x-z$ is even → $xRz$ → Relation is transitive ✅
• R is reflexive, transitive and symmetric → it is an equivalence relation ✅

Example

Example Relation on R^2

$R^2,(x,y)R(a,b)$ if $x+y=a+b$

Is the relation reflexive? $\forall (x,y)\in R\times R:(x,y)R(x,y)$

• $(x,y)R(x,y)$ if $x+y=x+y$ → this is trivially true → The relation is reflexive ✅

Is the relation symmetric? $\forall (x_1,y_2),(x_2,y_2)\in R\times R,(x_1,y_2)R(x_2,y_2)\to (x_2,y_2)R(x_1,y_1)$

• Let $(x_1,y_1)R(x_2,y_2)$ then $x_1+y_1=x_2+y_2$
• then $x_2+y_2=x_1+y_1$
• so $(x_2,y_2)R(x_1,y_1)$ → the relation is reflexive ✅

Is the relation transitive? $\forall (x_1,y_1),(x_2,y_2),(x_3,y_3)\in R\times R:(x_1,y_1)R(x_2,y_2)\wedge (x_2,y_2)R(x_3,y_3)\to (x_1,y_2)R(x_3,y_3)$

• Let $(x_1,y_1)R(x_2,y_2)\wedge (x_2,y_2)R(x_3,y_3)$
• then $x_1+y_1=x_2+y_2\wedge x_2+y_2=x_3+y_3$
• so $x_1+y_1=x_3+y_3$
• so $(x_1,y_1)R(x_3,y_3)$ → the relation is transitive ✅

---

Anti-symmetry

Definition

It is not the negation of symmetry. A relation that cannot go in both directions

• $\forall x,y\in A:(xRy\wedge yRx)\to x=y$
• $\forall x,y\in A:(xRy\wedge x\ne y)\to x!Rx$

Examples

• $xRy$ if $x\le y$ on $\mathbb{R}$ → Anti-symmetric ✅
• $xy$ if $x\le y+10$, on $\mathbb{N}$
  • Not symmetric: $x=1,y=20$ then $xRy$, since $1\le 20+10$, but $x!Ry$, since $20\le 1+10$ ❌
  • Not anti-symmetric: $x=1,y=2$, then $xRy$ since $x\le 2+10$ and $yRx$ since $2\le 1+10$ ❌
• $xRy$ if $x=y+10$ , on $\mathbb{N}$ → Anti-symmetric ✅
  • assume $xRy$ and $x\ne y$
    • then $x=y+10⟹y=x-10\ne x+10$
    • so $y!Rx$

Symmetry vs. Anti-symmetry

• Symmetry → all arrows go in 2 directions
• ==Anti-symmetry== → arrows between different elements cannot go in both directions

---

Partial order

Definition

A relation that is reflexive, transitive and anti-symmetric is called a partial order

Examples

• Subset Relation → $\subseteq ,on\mathbb{P}(\mathbb{N})$

  • Reflexive → $\forall$ set A $\in \mathbb{P}(\mathbb{N}):A\subseteq A$ ✅
    • Every set is a subset of …
  • Anti-symmetry → if $A\subseteq B\wedge B\subseteq A⟹A=B$ (set equality) ✅
  • Transitive → if $A\subseteq B\wedge B\subseteq C⟹A\subseteq C$ ✅
    • Let $x\in A$
    • $⟹x\in B$ since $A\subseteq B$
    • $⟹x\in C$ since $B\subseteq C$

• $xRy$ if $x\le y$, on $\mathbb{R}$

  • Reflexive → $x\le x$ true (every number is smaller/equal than itself) ✅
  • Anti-symmetry → if $x\le y\wedge y\le x⟹x=y$ ✅
  • Transitive → $x\le y\wedge y\le z\to x\le z$ ✅

• $xRy$ if $x$ is a multiple of y, on $\mathbb{N}$

  • Reflexive → $xRx$ if x is a multiple of x → true for $\forall x\in \mathbb{N}$ (every number is a multiple of itself) ✅
  • Anti-symmetry → $xRy\wedge yRz\to xRz$
    • $xRy$ so $x=ky$ $(k\in N)$
    • $yRz$ so $y=mz$ with $m\in N$
    • then $x=k(mz)=(km)z$ so $xRz$ ✅
  • Transitive → $xRy\wedge yRx$
    • $⟹x=ky\wedge y=mx⟹x=kmx$
    • $⟹k=m=1⟹y=x$ ✅

---

Total order

Note

Not exam material

• What is the difference between a partial order and a total order?
  • Partial order → Transitive, Anti-symmetric, reflexive
  • Total order → Partial order + $\forall x,y\in A:xRy\vee yRx$

---

Key takeaways

• Do you know what anti-symmetry is?
• Do you understand that symmetry and anti-symmetry are NOT opposites?
• Do you know when a relation is a partial order. (and how to prove this)?

---

Lecture slides

Lecture 7

Lecture 8

Extra materials