BCS1130-9 Function properties

Lecture notes

• Injective functions
  • Proving that a function is injective:
• Surjective functions
  • Proving that a function is surjective
• Bijections
  • Proving a function is bijective
• Inverse functions

---

Injective functions

Definition

A function $f:A\to B$ is injective if two different elements have different function values (Funzione iniettiva, every element of the domain is mapped to a different value of the codomain)

Formal definition: A function $f:A\to B$ is injective if $(\forall x,y\in A)(x\ne y⟹f(x)\ne f(y))$ Contrapositive: $\forall x,y\in A,(f(x)=f(y)⟹x=y)$

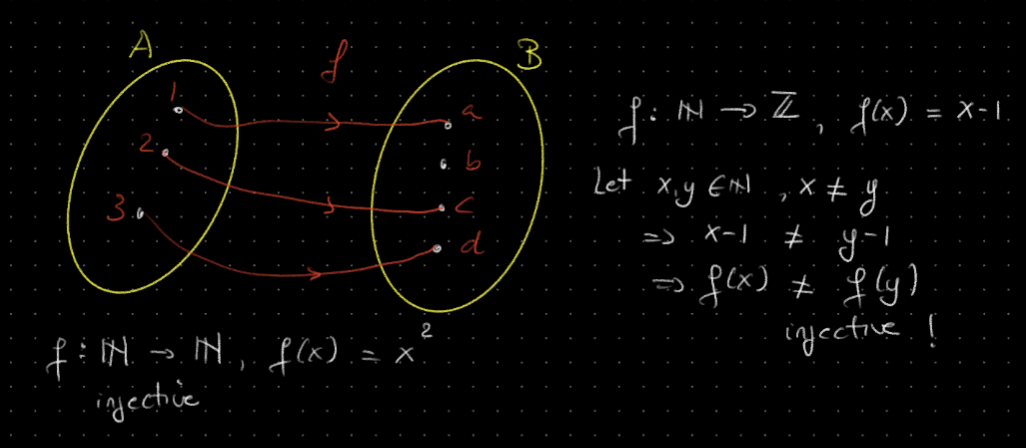
Proving that a function is injective:

$f:\mathbb{N}\to Z,f(x)=x-1$ → prove that it is injective

• Let $x,y\in N,x\ne y$
  • $⟹x-1\ne y-1$
  • $⟹f(x)\ne f(y)$ → Injective ✅

$f:Z\to Z,f(x)=x^2$ → prove that it is not injective

• Not injective, since $1\ne -1,f(1)=f(-1)$ ❌

$f:N\to N,f(x)=x^2$ → this is injective ✅

Surjective functions

Definition

A function $f:A\to B$ is surjective if every element of B is the image of an element of A → the range is equal to the codomain (each element of the codomain has been mapped from at least an element of the domain)

Formal definition: A function $f:A\to B$ is surjective if $(\forall y\in B)(\exists x\in A)(y=f(x))$

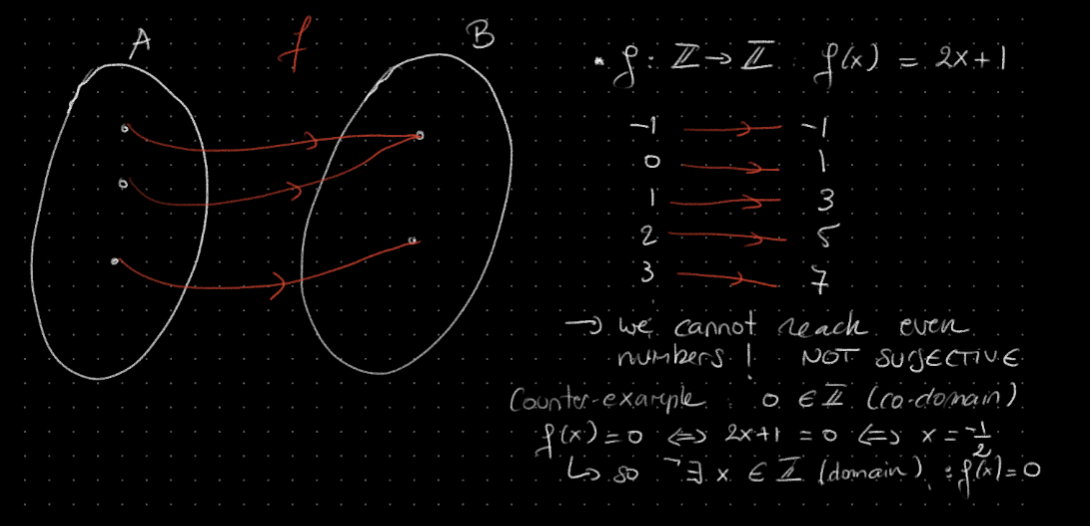
Proving that a function is surjective

Warning

We can usually prove that a function is not surjective by finding a counterexample

Example 1 $f:Z\to Z,f(x)=2x+1$

• $o\in Z,o=2x+1⟹x=-\frac{1}{2}$
• $-\frac{1}{2}\notin Z$ ❌

Example 2

$$\begin{array}{c}f:\mathbb{Z}\to zf(x)=\{\begin{array}{l}-\frac{x-1}{2},x,odd\\ -\frac{x}{2},x,even\end{array}.\end{array}$$

We use one of the definitions, for example the definition of f(x) when x is even

• Let $y\in Z,y=-\frac{x}{2}$
  • $⟹x=-2y$, so x is even
  • $⟹$ with x even, $f(x)=-\frac{(-2y)}{2}=y$

We can also use the other definition:

• Let $y\in Z,y=-\frac{x-1}{2}$
  • $\to x=-2y+1$ so x is odd
  • $⟹f(x)=f(-2y+1)=\frac{2y-1+1}{2}=y$

Example 3

• take detailed notes of this example $f:\mathbb{P}(A)\to \mathbb{N}\cup \{o\},f(B)=|B|$
• $A=\{0,1\},P(A)=\{\varphi \}$

Bijections

Definition

A function $f:A\to B$ is a bijection if it is injective and surjective (Each element of the domain is mapped to exactly 1 element of the codomain)

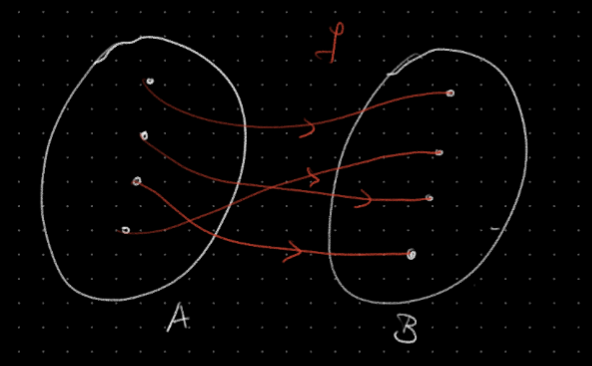
Proving a function is bijective

Example 1 $f:N\to N,f(x)=3x-4$

• Not a properly defined function!
• Since $1\in N$ (domain), but $f(1)=-1\notin N$ (co-domain)

Example 2 $f:Z\to Z,f(x)=3x-4$

• Check if it is injective: $\forall x_1,x_2\in Z:x_1\ne x_2⟹f(x_1)\ne f(x_2)$ (def)
  • Let $x_1,x_2\in Z,x_1\ne x_2$
  • then $3x_1-4\ne 3x_2-4$
  • so $f(x_1)\ne f(x_2)$ → Injective ✅
• Check if it is surjective: $\forall y\in Z:\exists x\in Zy=f(x)$ (def)
  • Disproof by counter example
  • $0\in Z$ (co-domain) → $0=f(x)$
  • $⟺0=3x-4$
  • $⟺x=\frac{4}{3}\notin Z$ → x is not in the domain, f is not surjective ❌

The function is not bijective ❌

Example 3 $f:R\to R,f(x)=3x-4$

Check if it is injective

• Let $x_1,x_2\in R,x_1\ne x_2$
  • then $x{3}_1-4\ne 3x_2-4$
  • so $f(x_1)\ne f(x_2)$ → Injective ✅

Check if it is surjective

• Let $y\in R$ (co-domain)
  • $y=f(x)=3x-4⟺x=\frac{y+4}{3}$
  • choose an $x=\frac{y+4}{3}\in R$
  • ( $y=f(x)=3x-4⟹x=\frac{y+4}{3}$)
  • and $f(x)=3(\frac{y+4}{3})-4=y$ → Surjective ✅

Then the function is bijective ✅

---

Inverse functions

Definition

The inverse of a function reverses the function (inverting all the arrows). A function needs to be bijective for the inverse function to be properly defined

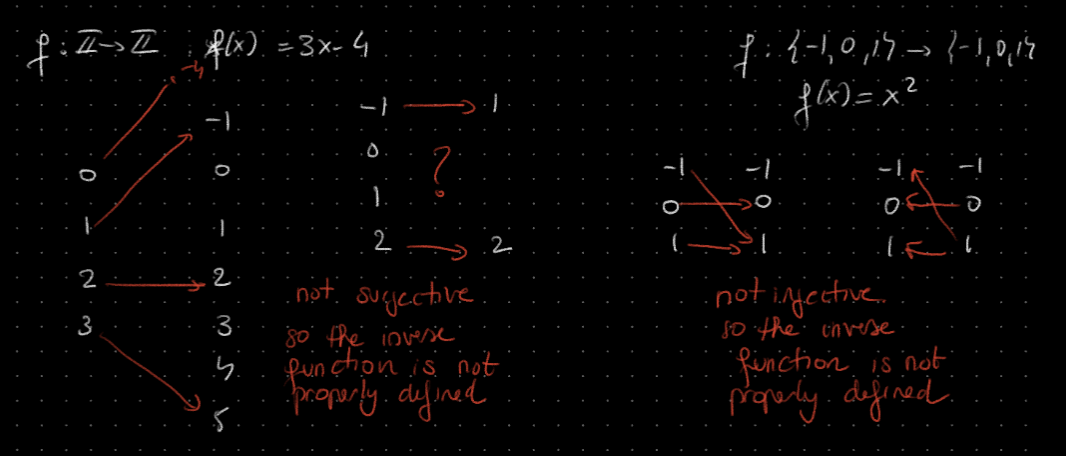
Example

$f:R-\{2\}\to R,f(x)=\frac{1}{x-2}$

Calculating the inverse

1. We start by calculating the inverse function
   1. $y=f\left(x\right)=\frac{1}{x-2}\iff x-2=\frac{1}{y}\iff x=\frac{1}{y}+2$
   2. so $f^{-1}\left(y\right)=\frac{1}{y}+2$
2. Is $f^{-1}(x)$ is defined on domain $R$ (co-domain of $f$)?
   1. No, it is defined for $y=0$
   2. $⟹f:R-\{2\}\to R-\{0\},f(x)=\frac{1}{x-2}$
3. We adjust the domain of $f^{-1}$ so that they are both inverse functions of one another, making them bijective
   1. $f:\mathbb{R}-\left\{2\right\}\to \mathbb{R}-\left\{0\right\},f\left(x\right)=\frac{1}{x-2}$
   2. $f^{-1}:\mathbb{R}-\left\{0\right\}\to \mathbb{R}-\left\{2\right\},f^{-1}\left(x\right)=\frac{1}{y}+2$

Checking the inverse function

\left( 2\right) f^{-1}\left( f\left( x\right) \right) ,x\in \mathbb{R} -\left\{ 2\right\} \end{aligned}$$ ## Key takeaways - Do you know what injective, surjective means? - Can you prove that a function is injective? - Can you prove that a function is surjective? - Do you know what a bijection is? - Do you understand that only bijective functions are invertible? - Do you know how to check that a function is the inverse? - - - ## Lecture slides ![[Attachments/DM-L9 Discrete Mathematics.pdf]]