BCS1130-4 Proof by induction

Lecture slides

Lecture notes

Can you calculate the sum 1+2+3 + ….+ (n-1) + n (with n a natural number)

• ${\sum }_{i=1}^n(i)=1+2+\cdots +n=\frac{n}{2}(n+1)$
  • We can demonstrate this with a few examples
  • Or we can demonstrate it through mathematical induction

Mathematical induction theory

Mathematical induction

Proof technique for statements of the form $\forall n\ge N,n\in Z$ (set of integers from a starting point on, e.g. natural numbers)

• Two steps in the proof by induction:
  • Base case (proof of $P(n)$) → the statement holds for the first number
  • Induction step: proof of $\forall n\ge N(P(n)\to P(n+1))$
• Process of induction
  • $P(n)$ is true → base case
  • $P(n)\to P(n+1)\forall n$ → (induction step)
  • $P(n),P(n)\to P(n+1)⟹P(n+1)$

Induction example

Induction example

$\forall n\in N\left({\sum }_{k+1}^{n}k=\frac{n(n+1)}{2}\right)$ Base case: Proof of P(1)

• ${\sum }_{k=1}^1=1=\frac{1(1+1)}{2}=1$ → This holds

** Induction step**: Proof of $\forall m\ge 1,p(m)\to P(m+1)$

• $p(m):{\sum }_{k=1}^{m}k=\frac{m(m+1)}{2}$ (assumption)
• $p(m+1):{\sum }_{k=1}^{m+1}k=\frac{(m+1)(m+2)}{2}$ (to prove)

• ${\sum }_{k=1}^{m+1}k=(1+2+\dots .+m+(m+1))$
  • we see that $(1+2+\dots +m)=p(m):{\sum }_{k=1}^{m}k=\frac{m(m+1)}{2}$
• We use our assumption
  • ${\sum }_{k=1}^{m+1}k=(1+2+\dots .+m+(m+1))=\frac{m(m+1)}{2}+(m+1)$
  • $=(m+1)\left(\frac{m}{2}+1\right)=(m+1)\left(\frac{m+2}{2}\right)$

Induction example 2

Induction example 2

$\forall n\in N:4^n-1$ is divisible by $3$

Base case: Proof of $P(1)$

• $P(1)=4^1-1=3$ → 3 is divisible by 3$

Induction step: Proof of $P(x)\to P(x+1)\forall x\in N$

• $P(x):4^x-1$ is divisible by 3 (assumption / hypothesis)
• $P(x+1):4^{x+1}-1$ is divisible by 3 (to prove)

Always use your assumption hypothesis!

• $P(x+1)=4^{x+1}-1=4\cdot 4^x-1=3\cdot 4^x+4^x-1$
  • $4^x-1$ is divisible by 3 by assumption ($3k$) → $4^x-1=3k$
  • $3\cdot 4^x$ is also a multiple of 3
• $P(x+1)=3\cdot 4^x+4^x-1=3\cdot 4^x+3k=3(4^x+k)$ → multiple of 3

Induction example 3

Induction example 3

A country has two types of coins: 3 cents and 7 cents. Prove that you can make all sums of money starting from 12 cents (up to 1 cent accuracy) from these coins.

Explaining the example $2\cdot 7=5\cdot 3$

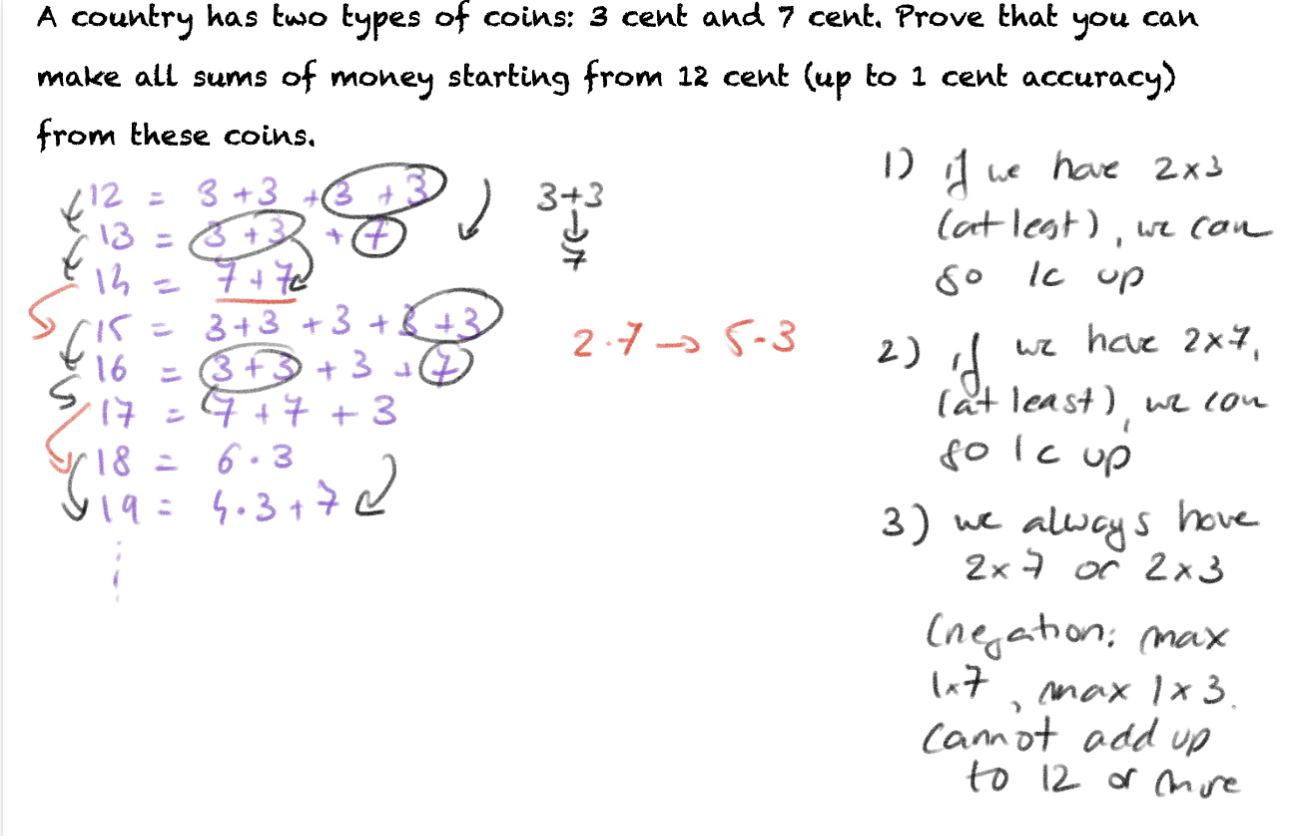
Negation: max 1x7, max 1x3 → cannot add up to 12 or more

1. If we have 2x3 (at least), we can go 1 cent up
2. If we have 2x7 (at least), we can go 1 cent up
3. We always have to have either (or both) 2x7, or 2x3

Proof by induction

• Base case: $P(12)$ holds → $12=3+3+3+3$
• Inductive step: $P(q)\to P(q+1)$
  1. q has at least 2 coins of 7 or 2 coins of 3
     • r: at least 2 coins of 7
     • s: at least 2 coins of 3
     • $\neg (r\vee s)=\neg r\wedge \neg s$ is impossible, as q ≥ 1
  2. if r is true, then we can replace 3x7 by 5x3
  3. if s is true, then we can replace 2x3 by 7
  • → in both cases, we can make q + 1

Induction example 4

An example like this won’t show up in the exam

Induction example 4 (Disproving with induction)

$\forall x\in N,\exists y\in N:x^y<y^x$ Counterexample: x = 3 To prove: $\exists x\forall y\in N:3^y\ge y^3$ (negation of the statement, with x=3)

Base case: $y=1\to 3^1\ge 1^3$ → this is true $y=2\to 3^2\ge 2^3$ → true $y=3\to 3^3=3^3$ → true

Induction step: if $3^k\ge k^3⟹(3^{k+1}\ge (k+1{)}^3)$ for all $k\ge 3$