BCS1110-6 Theory of Computation (2)

Lecture notes

• Lecture contents
• Deterministic finite automaton
• Tabular DFA
• Regular languages - Introduction - Complement of a language - Complementing regular languages - Closure properties
• Nondeterministic finite automaton - NFA Acceptance - [[#$ϵ$- Transitions|$ϵ$- Transitions]]
• Designing NFAs - Introduction - Guess and check
• Difference between NFAs and DFAs

Lecture contents

• Tabular DFAs
• Regular Languages
• NGAs
• Designing NFAs
• Tutorial Questions

Deterministic finite automaton

Formal definition

$D=(Q,\Sigma ,\delta ,q_0,F)$

• D → Automaton
• Q → Set of states
• $\Sigma$ → alphabet
• $\delta$ → Transition function
• $q_0$ → Start state
• F → Accepting state

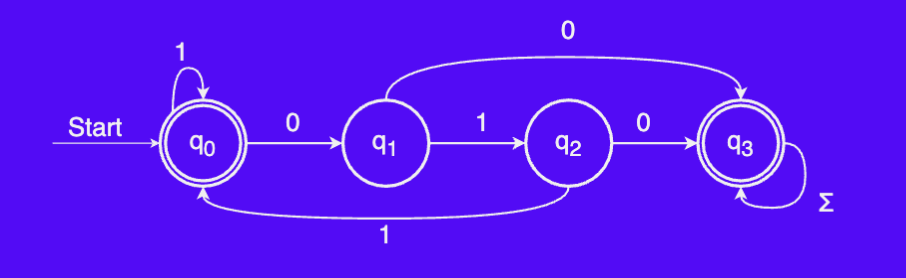
Tabular DFA

Tabular representation of the transactions in a deterministic finite automaton

Possible exam question

A possible exam question is to draw up the tabular representation of a DFA

Regular languages

Introduction

Definition

A language L is called a regular language if there exists a DFA D such that $L(D)=L$ If L is a language and L(D) = L, we say that D recognizes the language L

---

Complement of a language

Definition

Given a language $L\subseteq \Sigma \ast$, the complement of that language ($L’$) is the language of all strings in $\Sigma \ast$ that aren’t in L: $L^{\prime }=\Sigma \ast -L$

Complementing regular languages

• $L=\{w\in \{a,b\}\ast |$ w contains aa as a substring $\}$
• $L=\{w\in \{a,b\}\ast |$ w does not contain aa as a substring $\}$

Closure properties

Theorem

If L is a regular language, then L’ is also a regular language. As a result, we say that the regular languages are *closed under complementation

Nondeterministic finite automaton

Definition

An NFA is a Nondeterministic Finite Automaton. Structurally similar to a DFA, but represents a fundamental shift in how we’ll think about computation

• Nondeterministic computational model → Computing machine may have multiple decisions that it can make at one point. The machine accepts if any series of choices leads to an accepting state (Existential nondetermi anism)

Example of an NFA: 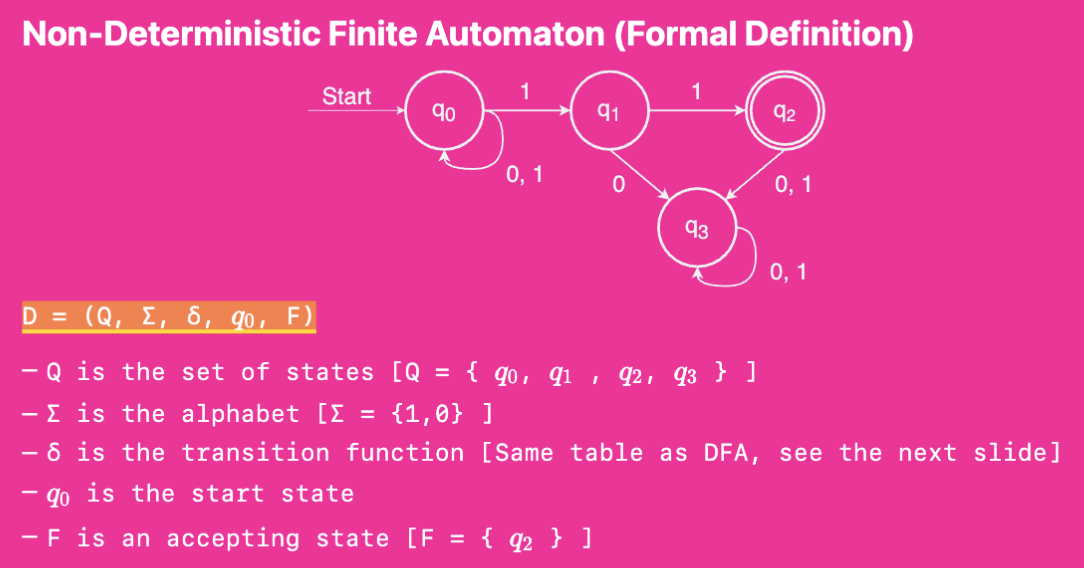→ The only difference in the formal definition of a NFA from an DFA is the transition function.

NFA Acceptance

Definition

An NFA N accepts a string w if there is some series of choices that lead to an accepting state. An NFA rejects a string w if no possible series of choices lead it into an accepting state.

• There is a difference between reaching a non-accepting state and to die:
  • NFA Rejecting a string → all inputs are processed but the NFA ends in a non-accepting state
  • NFA Dies → When executing a string, the NFA reaches a point where it can not process further input

$ϵ$- Transitions

Definition

An NFA may follow any number of $ϵ$-transitions at any time without consuming any input. NFAs are not required to follow such transitions.

Designing NFAs

1. Understand the Language: Before designing the NFA, make sure you understand the language or the set of strings you want the NFA to recognize.
2. Start Simple: Begin with a basic structure. If you’re designing an NFA for a language that accepts strings ending in ‘01’, start with that basic requirement.
3. Use ε-Transitions: One of the powers of NFAs is the ability to move from one state to another without consuming an input symbol, using ε-transitions. This can simplify your design in many cases.
4. Multiple Transitions: Remember that for a given state and input symbol, an NFA can have transitions to multiple states. Use this feature to represent multiple possibilities.
5. Avoid Overcomplicating: Just because you can have multiple transitions doesn’t mean you always should. If a simpler design works, go with it.
6. Design Incrementally: If you’re trying to design an NFA for a complex language, break the problem down. Design smaller NFAs for simpler languages and then combine them.
7. Use Sub-automata: For complex languages, design sub-automata for different parts of the language and then connect them using ε-transitions.
8. Test with Strings: Once you’ve designed your NFA, test it with various strings to ensure it accepts those it should and rejects those it shouldn’t.
9. Convert to DFA (Optional): If you find creating a NFA difficult, maybe you can solve the problem using a DFA, remember that any NFA can be converted to an equivalent DFA.

Difference between NFAs and DFAs

• Any language that can be accepted by a DFA can be accepted by an NFA
  • (Every DFA is technically an NFA)
• Any language accepted by an NFA can also be accepted by a DFA

---

Lecture slides