BCS1130-5 Set theory

Lecture notes

• Intro notation
• Describing sets
• Subsets
• Set equality
• Union, intersection, difference of sets
• Complement of a set
• Proofs with sets
• Associativity
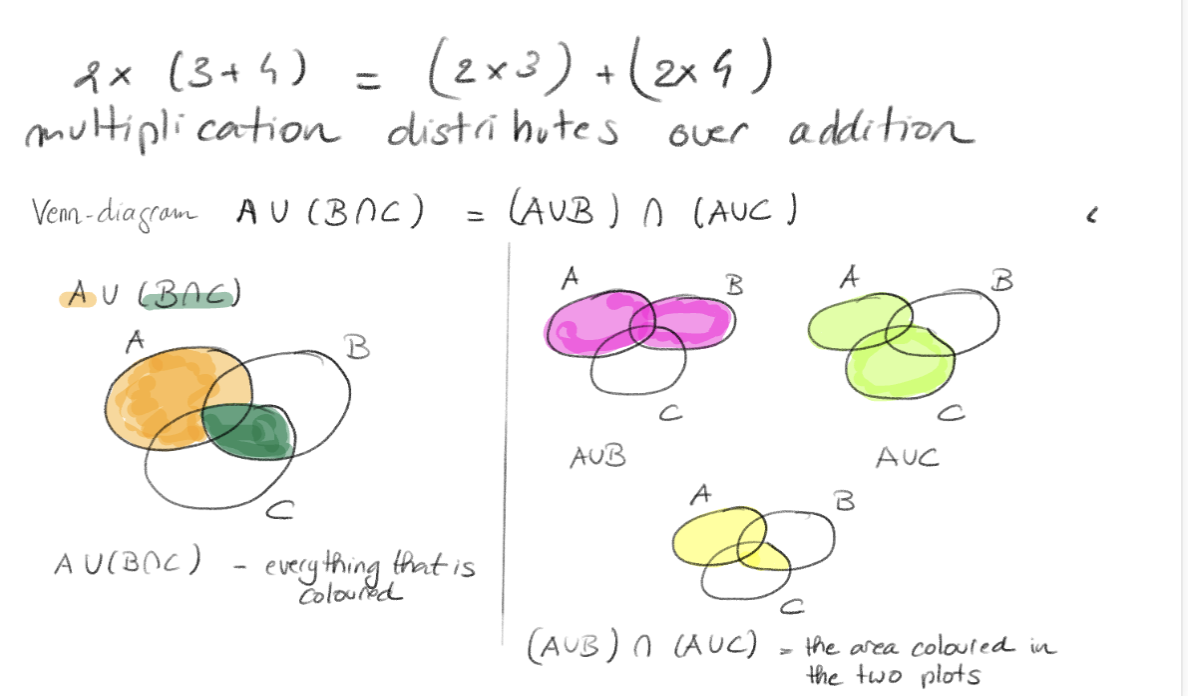
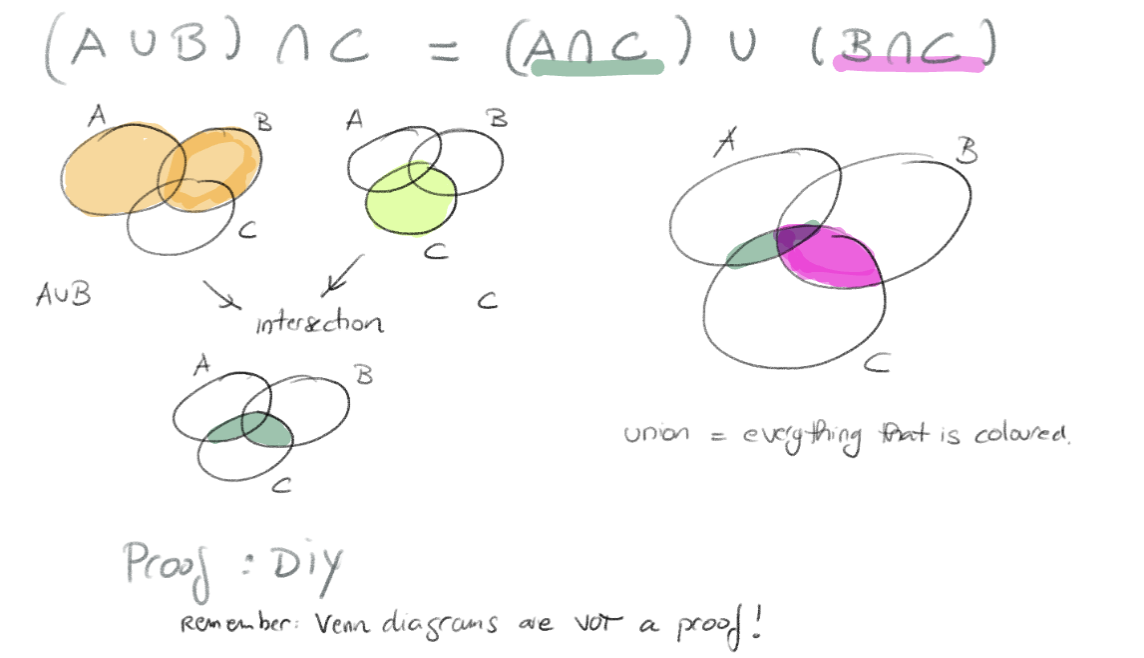
• Distributive laws
• De Morgan laws

---

Intro notation

• Set → Collection of specified, unordered and not duplicate objets. Can be infinite or finite or empty: $\{1,2,3,4\}$ or $\{\}$ (empty set can also be represented with $\varphi$ )
• Cardinality of a set → Number of elements in the set: $|\{1,2,3,4\}|=4$

Describing sets

• $A=\{x\in N:x<5\}$
• $A=\{1,2,\}$ → $\{1\}\subseteq A$

Subsets

Subset

The set B is a subset of the set A $⟺$ every element of B is also an element of A: $B\subseteq A$ $B\subseteq A⟺\forall x\in B:x\in A$ $B\subseteq A⟺\forall x:x\in B⟹x\in A$

B is a subset of A. B is not an element of A.

• $B=\{x:x\in DACS\}$
• $A=\{x:x\in UM\}$

The following statements are always true:

• $\varphi \subseteq A$
• $A\subseteq A$

Set equality

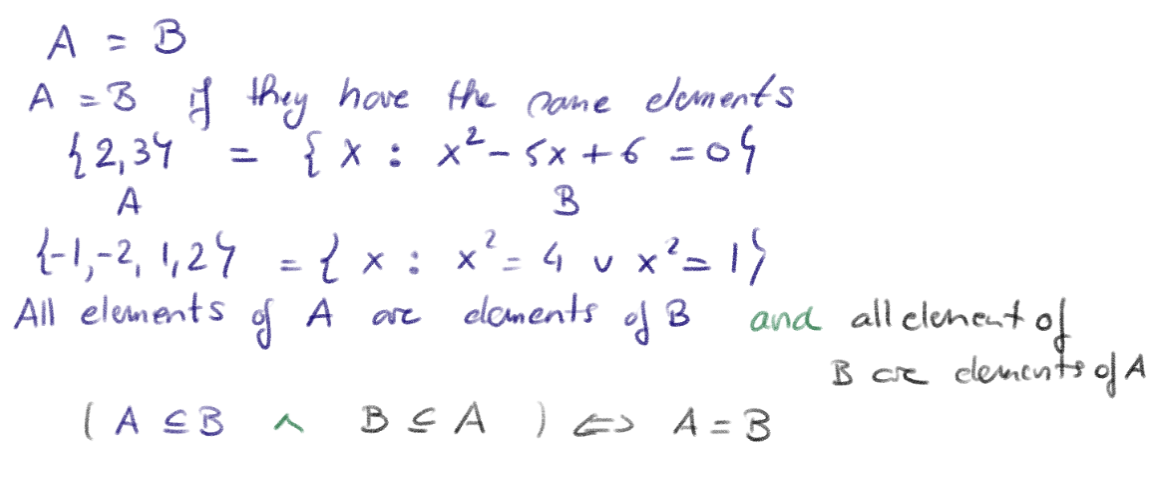
Union, intersection, difference of sets

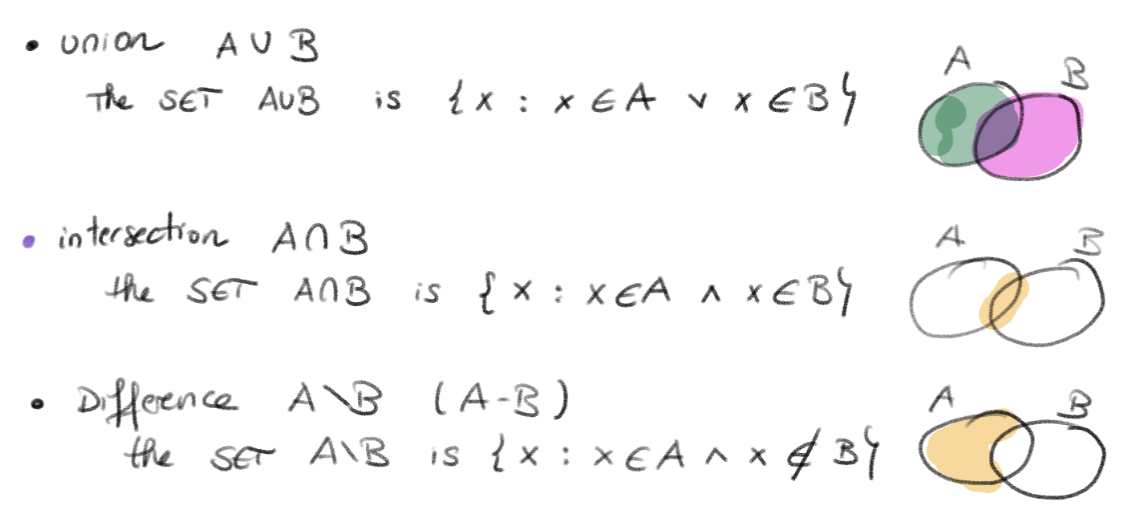
Complement of a set

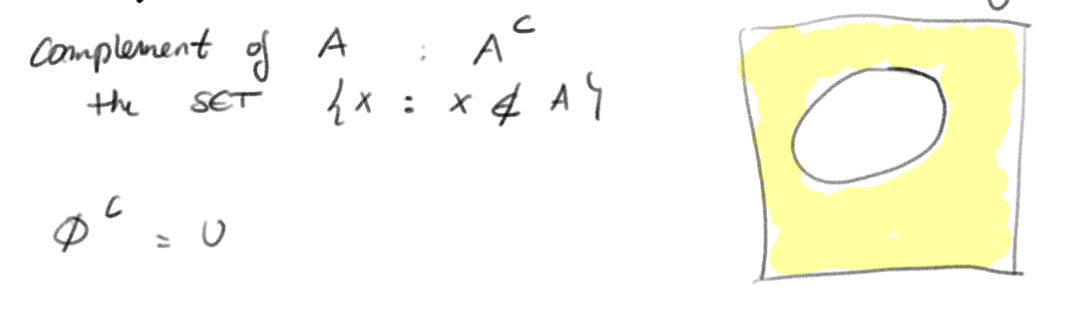
Proofs with sets

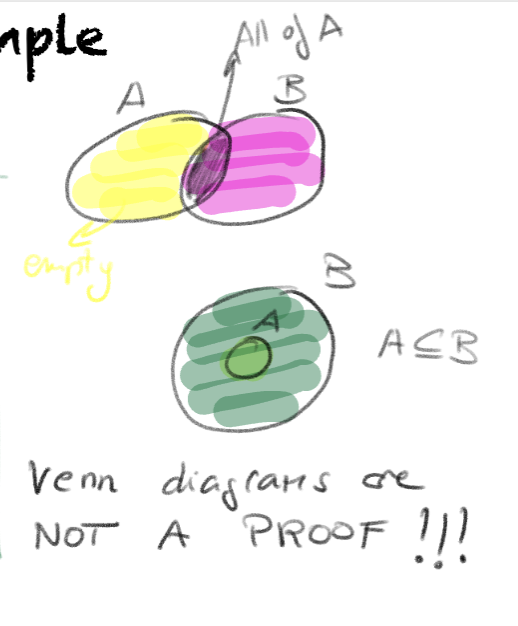
Example

$A\subseteq B⟺A\cup B=B$

1. $A\subseteq B⟹A\cup B=B$
2. $A\cup B=B⟹A\subseteq B$

First implication $A\subseteq B⟹A\cup B=B$

1. $B\subseteq A\cup B$
   • Let $x\in B$
     • then $x\in B\wedge x\in A$
     • then $xin(A\cup B)$
2. $A\cup B\subseteq B$
   • Let $x\in A\cup B$
     • then $x\in A\vee x\in B$
     • if $x\in A⟹x\in B$ since $A\subseteq B$
     • if $x\in B⟹x\in B$

• $⟹(A\cup B\subseteq B)\wedge B\subseteq (A\cup B)$
• $⟹A\cup B=B$

Second implication $A\cup B=B⟹A\subseteq B$

• Let $x\in A$
  • then $x\in A\vee x\in B$
  • then $x\in (A\cup B)$
  • then $x\in B$
  • $⟹A\subseteq B$

Associativity

• Intersection is associative: $A\cap (B\cap C)=(A\cap B)\cap C$
• Union is associative: $A\cup (B\cup C)=(A\cup B)\cup C$

Distributive laws

1. $A\cup (B\cap C)=(A\cup B)\cap (A\cup C)$
2. $A\cap (B\cup C)=(A\cap B)\cup (A\cap C)$

De Morgan laws

1. $(A\cup B{)}^c=A^c\cap B^c$
2. $(A\cap B{)}^c=A^c\cup B^c$

Key takeaways

• Do you understand how set membership works?
• Do you understand the definition of a subset, and how to prove that set A is a subset of B?
• Do you understand the meaning of intersection, union, complement, difference of sets?
• Do you know how to use Venn diagrams to help develop an intuition?
• Do you know how to prove that two sets are equal?

---

Lecture slides