BCS1130-6 Set theory

Lecture notes

• Proof example
  • First implication
  • Second implication
• Proof example (shorter)
• Proof example (truth table)
• Power set
  • Example of power sets
  • Cardinality of a power set
• Product sets
  • Example of product sets
  • Cardinality of product sets
  • Properties
• Set partitions
  • Definition
  • How many partitions are there

---

Proof example

Proof example

For all sets A, B, C, $(B\cap (A^c\cup C{)}^c=\varphi )⟺(A\subseteq B^c\cup C)$

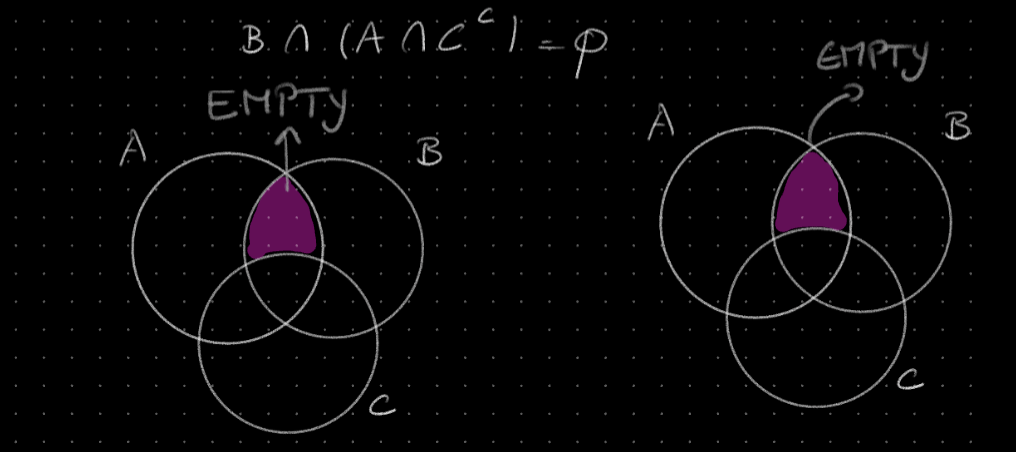
We try to prove that the statement is true (which we identified using Venn Diagrams)

First implication

$B\cap A\cap C^c=\varphi ⟹A\subseteq B^c\cup C$

• Let $x\in A$
  • Case 1: $x\in C$
    • $⟹x\in C\vee x\notin B⟹x\in B^c\cup C$
  • Case 2: $x\notin C$
    • Assume $x\in B⟹x\in A,x\in B\wedge x\notin C$
    • $x\in (B\cap A\cap C^c)$ → This is a contradiction as that set is empty
    • Therefore $x\notin B$ → $x\in B^x\vee x\in C⟹x\in B^c\cup C$

Second implication

$A\subseteq B^c\cup C⟹B\cap A\cap C^c=\varphi$ → We can either take the contrapositive, or take a contradiction

Proof by contradiction

• We need to assume the set $B\cap A\cap C^c$ is not empty → there is an element in that set: $x\in B\cap A\cap C^c$
  • then $x\in B,x\in A$ and $x\notin C$
  • so $(x\in B^c\vee x\in C)\wedge (x\in B\vee x\notin C)$ → Contradiction (the two sets are opposite)
  • so there is no $x\in B\cap A\cap C^c$ → the set $B\cap A\cap C^c$ is empty

Proof example (shorter)

Proof example

For all sets A, B, C, $(B\cap (A^c\cup C{)}^c=\varphi )⟺(A\subseteq B^c\cup C)$

We prove: $\neg (A\subseteq B^c\cup C)⟺\neg (B\cap (A^c\cup C{)}^c=\varphi )$

Subset: $\forall x\in A:x\in B$ Not subset: $\exists x\in A:x\notin B$

• $\neg (A\subseteq (B^c\cup C))$
  • $⟺\exists x\in A:x\notin (B^c\cup C)$
  • $⟺\exists x\in A:x\in (B^c\cup C{)}^c$ (if an element is not in something, it is an element of the complement)
  • $⟺\exists x\in A:x\in (B\cap C^c)$
  • $⟺\exists x:x\in A\wedge x\in B\wedge x\in C^c$
  • $⟺\exists x:x\in (A\cap B\cap C^c)$ → X is in the intersection of the three sets
  • $⟺(A\cap B\cap C^c)\ne \varphi$ → The set is not empty

Proof example (truth table)

Proof example

For all sets A, B, C, $(B\cap (A^c\cup C{)}^c=\varphi )⟺(A\subseteq B^c\cup C)$

---

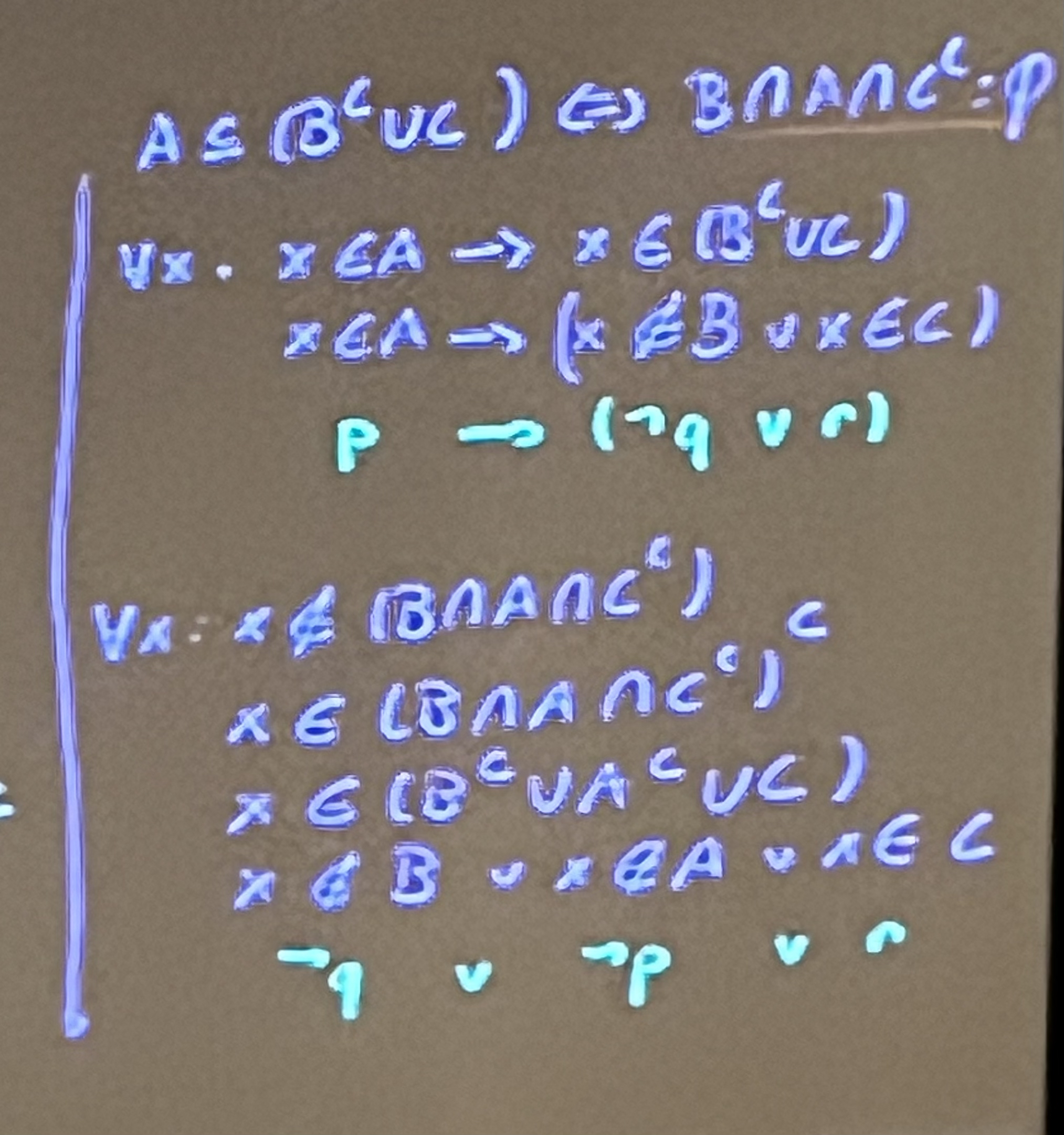
Power set

Power sets

A power set of a set A is the set of all subsets of A

Example of power sets

Example of a power set: $A=\{1,2,3\}$ $P(A)=\{\{1\},\{2\},\{3\},\{1,2\},\{1,3\},\{2,3\},\{\},\{1,2,3\}\}$ $|P(A)|=8$ (set size is 8)

Example of a power set: $B=\{i,\varphi \}$ $P(B)=\{\varphi ,\{1,\varphi \},\{1\},\{\varphi \}\}$

Cardinality of a power set

Size of a power set

$|P(A)|=2^{|A|}$

Product sets

Product sets

For two sets A and B, the product set $A\times B$ is defined as $\{(a,b)$ with $a\in A\wedge b\in B\}$

• $(a,b)$ is an ordered pair

Example of product sets

${\mathbb{R}}^2=\mathbb{R}\times \mathbb{R}$ → Cartesian plane

Cardinality of product sets

Cardinality of product sets

$|A\times B|=|A|\times |B|$

Properties

• $A\times B=B\times A$
  • when $A=B$
  • when one of the sets is empty → The product is also empty

Set partitions

Definition

Set partitions

The sets $A_1,\dots A_n$ form a partition of the set A $⟺$

1. None of the sets $A_k$ is empty: $A_k\ne \forall k$
2. $A_1\cup A_2\dots \cup A_n={\cup }_{k=1}^n{A}_k=A$
3. $A_m\cap A_k=\varphi$ if $m\ne k$

How many partitions are there

Partitions

$B_{n+1}={\sum }_{k=0}^n\left(\genfrac{}{}{0ex}{}{n}{k}\right)B_k$

Key takeaways

• Do you know how set membership works?
• Do you understand the meaning of the set operators (complement, intersection, union, difference)
• Do you know how to use Venn diagrams to develop an intuition
• Do you understand the concept and definition of subset?
• Do you know how to prove that two sets are equal?
• Do you understand how to use the associative, distributive and de Morgan Laws? Can you prove them?
• Do you know how to use power sets? Can you formulate the power set of a (finite) set?
• Do you understand how set product works?
• Do you know what a partition is?.

---

Lecture slides

Lecture slides

Partitions