BCS1110-5 Theory of Computation

Lecture notes

• Lecture contents and key points
• Introduction - Automata - Definition of problems - Finite automata
• Formal language theory - Important terms - String - Language - The model
• Finite automata
• FSA Examples
• Deterministic finite automaton

Lecture contents and key points

• Formal language theory
• Finite automata
• FSA Examples
• Recognizing languages with DFAs
• Deterministi Finite Automaton

Introduction

• TOC Attempts to answer the question of what problems we can solve with a computer (e.g. social problems)

Example: Halting Problem

Given a piece of code, can you write a piece code that can determine wether the first program will run indefinitely or not?

This problem was first proposed by Alan Turing

Automata

Automaton

An Automaton is an idealized mathematical computing machine. Usually used to solve relatively simple logical problems.

Why build models?

• ==Mathematical simplicity== → easier to manipulate models than actual computers
• Intellectual robustness → All computers can be thought of as special cases of a general model

Definition of problems

We need a definition of problems with specific characteristics:

• Corresponds to the problem we want to solve
• Captures a large class of problems
• Is mathematically simple to reason about but no one definition encapsulates all three problems

Finite automata

Finite Automata

A Finite automata are abstraction of computers with finite resources constraints

Finite State Automata:

• Deterministic Finite State Automata (DFA)
• Non-deterministic Finite State Automata (NFA)

Formal language theory

Important terms

• Alphabet → Set of characters
• Characters → Individual symbols, element of an alphabet
• Strings → Finite sequence of characters
• Language → Set of strings

String

• Informal definition→ Any sequence of any symbols (characters)
• Formal definition →
  • An alphabet ($\Sigma$) is a finite set of symbols called characters
  • A string over an alphabet $\Sigma$ is a finite sequence of characters drawn from $\Sigma$
    • For example, If $\Sigma =\{a,b\}$, a valid string over $\Sigma$ is ababababaaababab or a
  • The empty string has no characters and is denoted by $ϵ$

Language

• Informal definition→ A set of strings
• Formal definition:
  • A formal language is a set of strings
  • We say that L is a language over $\Sigma$ if it is a set of strings over $\Sigma$
  • The set of all strings composed from letters in $\Sigma$ is denoted as $\Sigma \ast$
  • Formally we say that L is a language over $\Sigma$ if $L\subseteq \Sigma \ast$

The model

Fundamental question

For what language L can you design an automaton that takes as input a string, then determines whether the string is in L?

Finite automata

Definition

A finite automaton is a simple type of mathematical machine for determining whether a string is contained within some language

• Finite → The automata has a stopping point, this is intended to mimic computer’s finite resources
• ==State== →
• Transition →
• Final/Accept State → If the automata ends in the accept state, the string is recognized and such string belongs to the automaton.

The language of an automaton is the set of strings that it accepts:

• If D is an automaton that processes characters from alphabet $\Sigma$, then $L(D)$ is formally defined as:
  • $L(D)=\{w\in \Sigma \ast |D$ accepts $w\}$

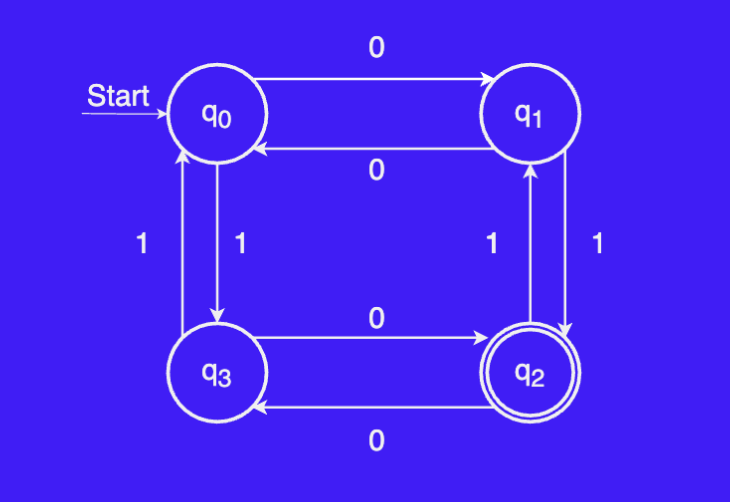
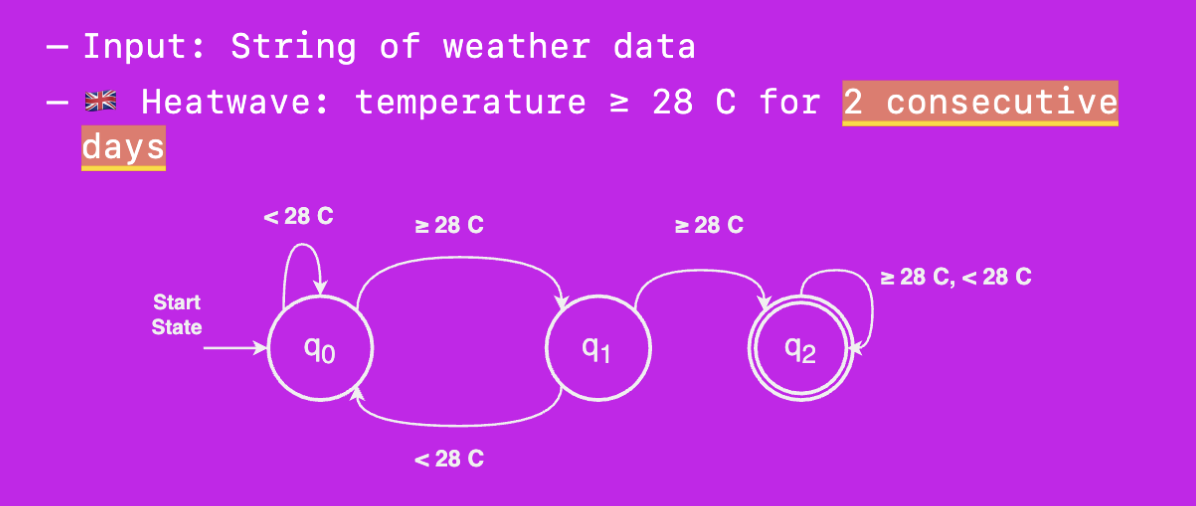
FSA Examples

Deterministic finite automaton

Definition

A DFA is defined relative to some alphabet $\Sigma$. For each state in the DFA, there must be exactly one transaction defined for each symbol in $\Sigma$ (Determinism).

A DFA has a unique start state and there are zero or more accepting states.

• Need for clearly defined routes and behavior in all cases in an Automaton
• These conditions need to be disallowed
  1. No transition out of a state on some input
  2. Multiple transitions out of a state on some input

---

Lecture slides